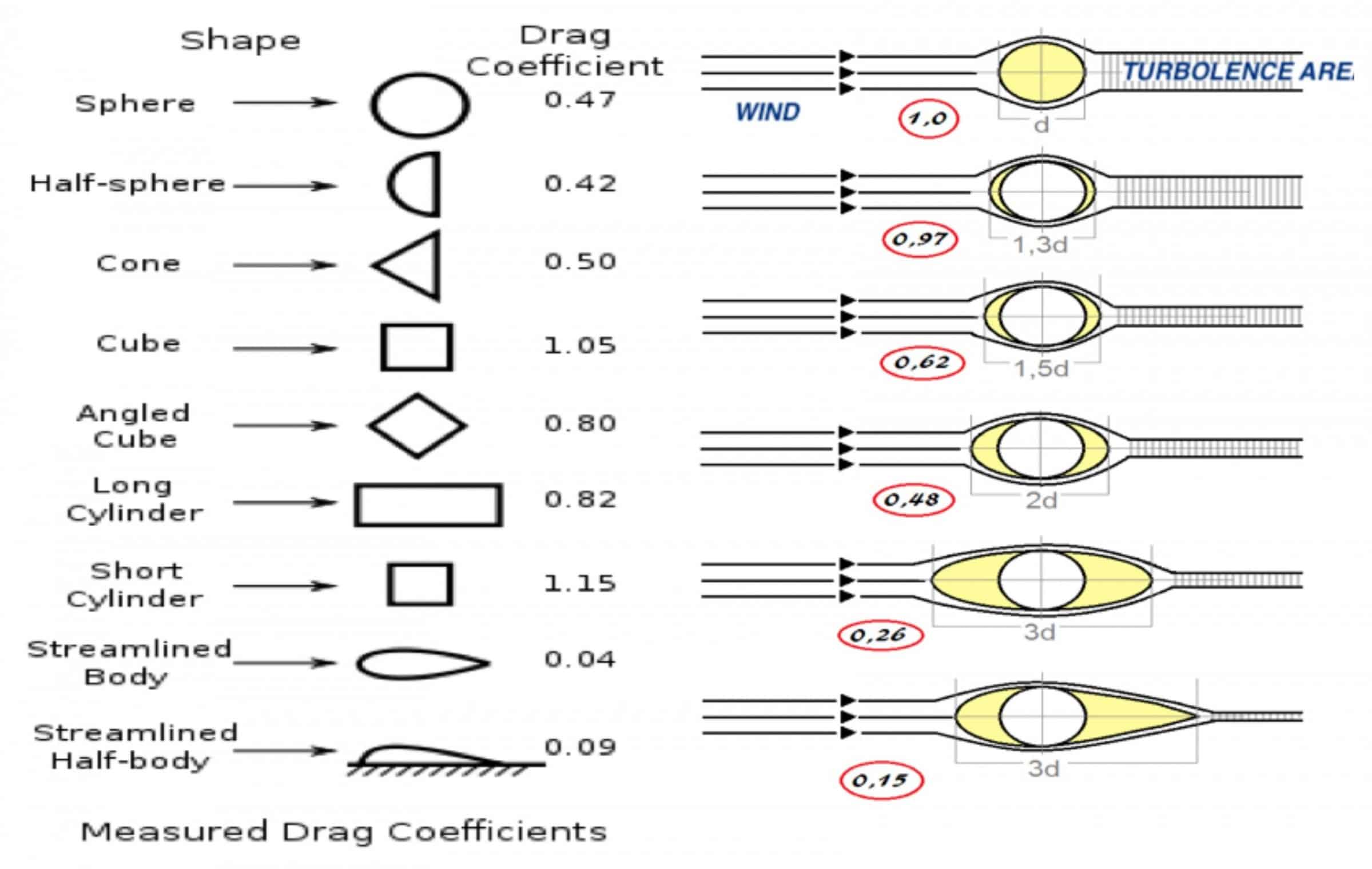
Drag coefficient of shapes
Pressure drag and shape factor
The shape factor and drag coefficient.
The motion of a body in a fluid, when it is quite slow, is “laminar“: the fluid moves, that is, as if it were made up of many thin sheets that are able to slide over each other. When the movement of the body in the fluid is fast, it assumes the definition of “turbulent” in that many small vortices are formed chaotically and the speeds differ considerably even for very close points, changing rapidly over time.
An appropriate shape of the object can therefore favor laminar motion. The latter guarantees the least resistance to progress and the best possible shape is given to us by nature: the drop. We analyzed the difference between laminar and turbulent flow here.
Common object: drag coefficient of shapes.
A liquid, in fall, spontaneously takes this form, which allows it to have as little resistance as possible from the air. Considering also the formula:
\(\begin{align*} \sqrt{\frac{mg}{\rho C_d S}}\end{align*} \)
where “m” is the mass of the object, “g” is the gravitational acceleration, “ρ” is the density of the air, “S” is the section of the object perpendicular to the falling motion and “Cd” is the coefficient of aerodynamic drag, it can be seen that to obtain a high limit speed it is therefore necessary to decrease Cd, which is found in the denominator.
In particular, a very low aerodynamic drag coefficient corresponds to a very high limit speed. To be updated with our contents, share and follow us (Facebook page here)