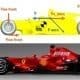
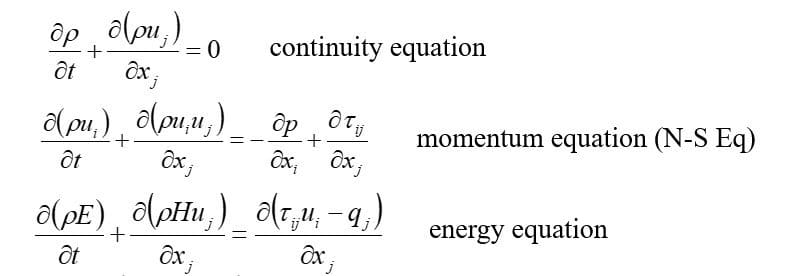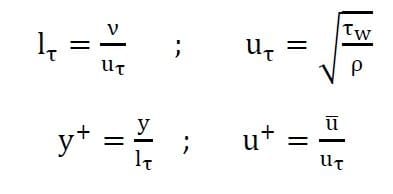Turbulent flow explained and boundary layer in Racing cars

What’s the difference between turbulent and laminar flow?

This lesson is going to be very technical and the main focus will be the distinction between laminar and turbulent flow. An incomplete definition of laminar flow may be “the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface” or in slightly different words: “laminar flow is characterized by fluid particles following smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing”.

In fact, there’s no complete agreement in the definition of turbulent flow, so its incompleteness reflect also on laminar condition definition.

When an air flow is turbulent?

In general, the flow can be referred as turbulent when:

• the process is random;
• turbulence involeves a wide range of spatial and temporal ranges;
• It arises at high Reynolds number;
• Turbulence is intrinsecally three-dimensional;
• Turbulence is a continuum phenomenon;
• Turbulence dissipates energy.

Reynolds number and turbulent flow.

A detailed lesson about turbulentce will be dedicated. However, we now need to define the Reynolds number.

\(\begin{align} Re=\frac{\rho v L}{\mu} \end{align} \)

where \( \rho \) is the density of the fluid, \( \mu \) is the dynamic viscosity, v is the velocity of the fluid and L is the characteristic length of the phenomena. This adimensionalized number refletc the ratio between inertia forces adn viscous forces. When a critical value of Reynolds number is reached the transition from laminar to tubulent flow begins. It is important to point out that the governing equations remain the same:

Which are the main regions of the turbulent boundary layer?

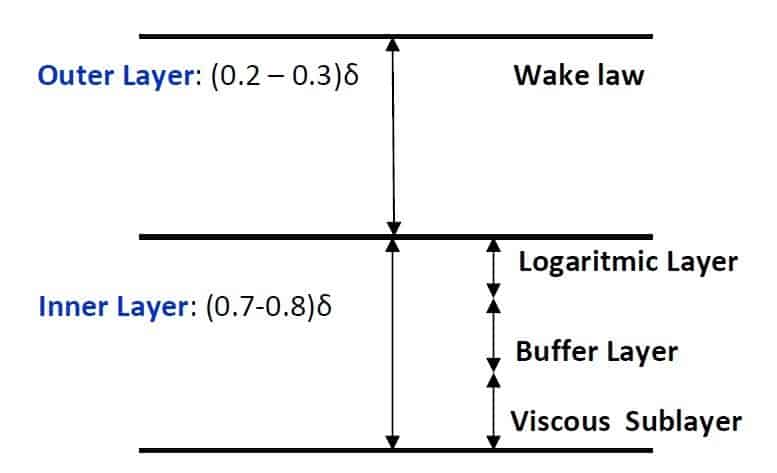
The boundary layer that develops in the turbulent flow can be divided in few significant regions:

• viscous sublayer where \( u^+=y^+ \)
• buffer layer, a transition region between viscous and log region;
• logarithmic region where  \( u^+=\frac{1}{k}ln\frac{yu_{\tau}}{\nu} +C \) where k=0.41 (Von Karman constant) anc C=5 (Coles constant)

The study of the turbulent boundary layer.

The schematic shows the different regions within a wall-bounded flow at typical laboratory and field Reynolds numbers. The inner layer includes the viscous sublayer and the log region. Between the two regions, from about y+=5 and y+=30 it is situated the so called buffer layer, where both the viscous stress and turbulence shear stress are important and where the peak production and dissipation of turbulence kinetic energy occur.

The definition of friction velocity and viscous length is given below.

In the log region the viscous stress is negligible, and (as it will be seen) the Reynolds stress is nearly constant.

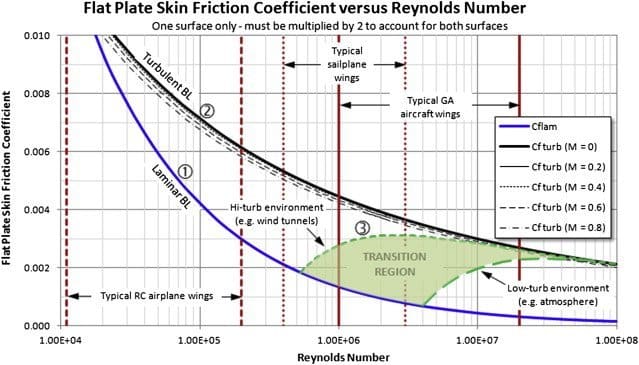
Value of skin friction for turbulent and laminar boundary layer.

The turbulence flow determines higher values of skin friction coefficient due to higher shear stresses. The trend of the skin friction (which produces an amount of drag) is reported in the image below.

Why therefore, laminar airfoil of laminar flows are not always preferred? Because the more energetic boundary layer of the turbulent flow can afford better adverse pressure gradient and delay the detachment of the flow. An example will follow in the next Lesson 4 about the Golf ball. Are you interested in buying vortex generator to reduce pressure drag?