Grip tyre and F1 telemetry
What are G-G diagram, pneumatic and mechanical trail
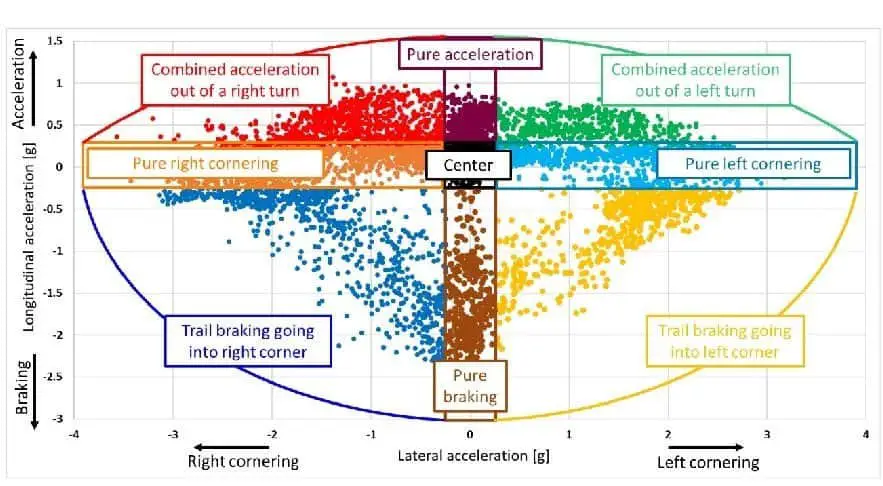
F1 telemetry data analysis: what is the g-g diagram.
Each track has its own peculiar features usually divided at first glance by high, medium or low downforce setup. The characteristics of the track require the engineers to choose a particular set of ride heights (front and rear). During the pre-seasonal tests and the free pratictises, a lot of data are provided by the F1 telemetry system (you can get some data of F1 telemetry by registering on F1 site here). An importat data to take is the amount of time spent in some particular condition.
What is the the g-g diagram?
For this reason, the g-g diagram reveals to be very useful.
How the tire behaves during his rolling is the main key to understand one of the most important tire diagram: the g-g diagram. This graph is determined by lateral and longitudinal forces functions of the total tire load.
As we said in previous chapter, the tyres are the unique source of torques and forces due to braking, cornering, accelerations, road banking and aerodynamics.
g-g diagram and forces.
All these forces are possible thanks to the basic grip with the ground.
Tires are too complex to consider as a whole, that’s the reason why we have to isolate and explain its characteristics separately.
First classification of forces is between lateral (generated by cornering that creates the aligning torque) and longitudinal (tractive and braking).
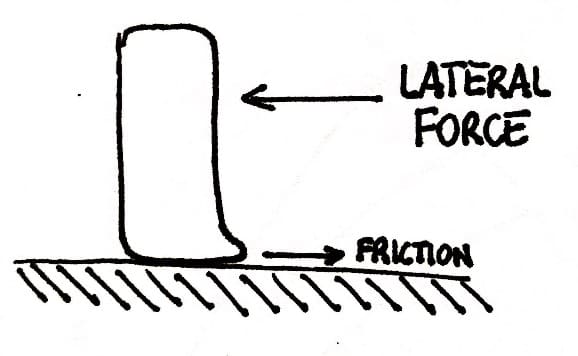
The lateral force is perpendicular to the direction in which the wheel is headed ignoring any inclination or camber.
For studying these forces, every tires, in every operating conditions, are associated to a vector representing the forces between tires and road. Every vector is divided into six components depending on reference axis system.
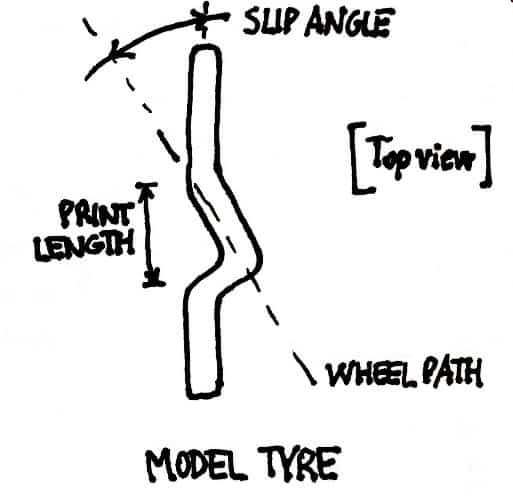
We have to start talking about the footprint, or simply “print”, the area of the tread of the tire that is in contact with the ground in any moment.
What is tyre GRIP.
The so called “grip” or handling between the footprint and the ground is given essentially by 2 phenomena:
- Molecular adhesion between the tread and the tarmac (or any other surface)
- Rubber elements stuck in the road between the little stones
- Elastic distortion of the rubber
The grip coefficient is defined by the relation: \(\begin{align} \mu=\frac{F_y}{F_z} \end{align} \)
where Fz is the vertical force and Fy the lateral one.
Important definition in tyre grip definition.
With a lateral force:
- Tyre deflects and moves laterally: more is the force more the rubber deflects until the tire begin sliding where the lateral force remained more or less constant.
Considering the rolling of the tyre (so there is a component to the back):
There is no sliding in the footprint except near the trailing edge where, obviously, the vertical forces are low.
We see from the picture the slip angle: it’s the angle between a rolling wheel’s actual direction of travel and the direction towards which it is pointing. In other words, it’s the difference between where car is pointing (heading) and where it’s actually going.
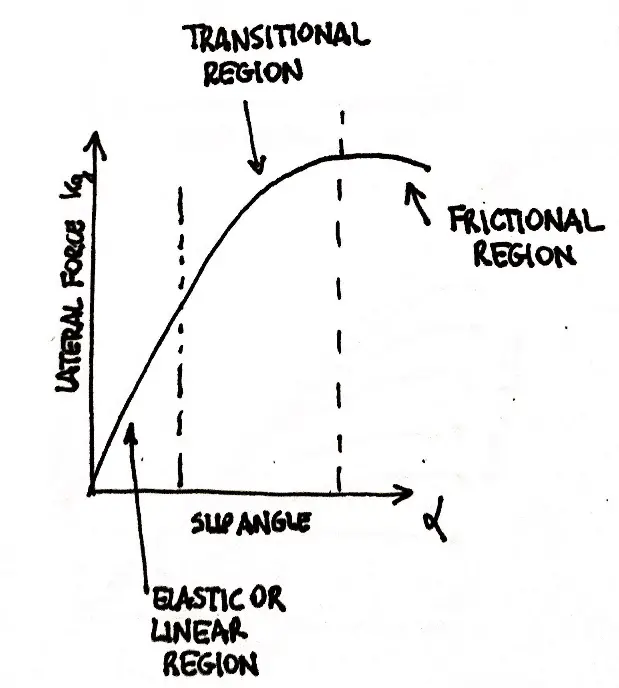
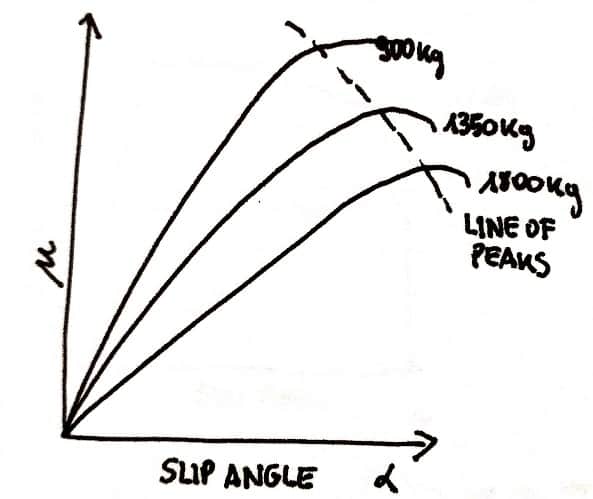
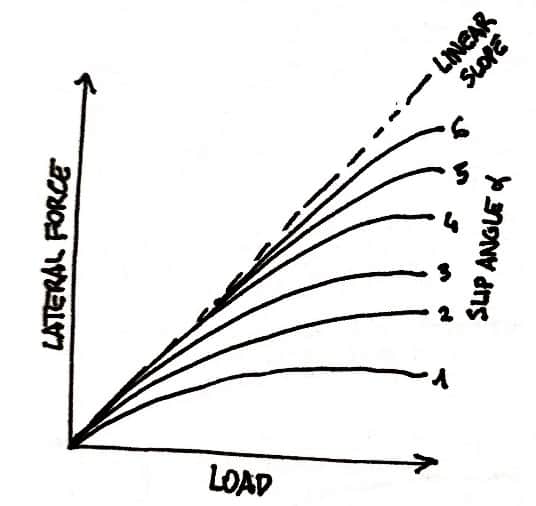
Tyre load sensitivity curves.
The tyre behaviour is described by very complicated models (we talked about them here). In fact, tyre performances are deeply influenced by the absolute value of vertical load. Moreover, the maximum tyre friction depends on the slip angle. These 2 data are embedded in the third graph ‘Lateral Force vs Load’. Of course, the aim of a faster car is to have the lateral force as higher as possible in order to drive inside the turns at much higher speed.
We can understand how the vertical loads in a car during a competition or simply in the city are constantly changing due to corner, acceleration, braking etc..so how complex is study the behavior of the tire in its motion.
Pneumatic trail: a stabilizing effect.
An effect of a lateral force is the aligning torque that’s the tendency of the tire to recover its natural rolling position and to steer around the z axis through the center of the print.
This is a stabilizing effect.
Whait is the pneumatic trail.
The aligning torque, like math and physics taught, is the product between a force (the lateral force) and a lever arm that in this case is called Pneumatic Trail and it’s the distance from the fore-aft center of the print to the center of action of the lateral force.
As the print is asymmetrical, the pneumatic trail is always present and so the aligning torque.
Pneumatic trail and aligning torque.
But the aligning torque is only one term of the steering torque, because there is another lever arm called mechanical trail given by the caster angle plus the position of the kingpin referred to the wheel center.
So, the steering torque can be defined as:
\(\begin{align} steering\,torque= aligning\,torque +mech_{trail}\cdot F_y \end{align} \)Or isolating Fy
\(\begin{align} steering\,torque= (pneu_{trail} +mech_{trail})\cdot F_y \end{align} \)