Modelli pratici di pneumatici: angolo di slittamento e rapporto di slittamento
Rapporto di slittamento e angolo di slittamento influenzano le prestazioni del veicolo
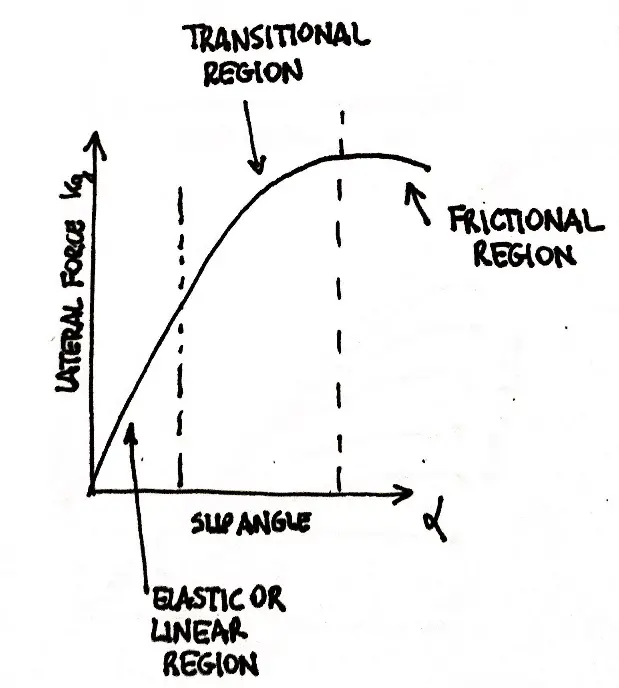
Forza longitudinale: rapporto di slittamento e angolo di slittamento.
Continuiamo il capitolo precedente parlando di forze longitudinali, rapporto di scorrimento e angolo di scorrimento.
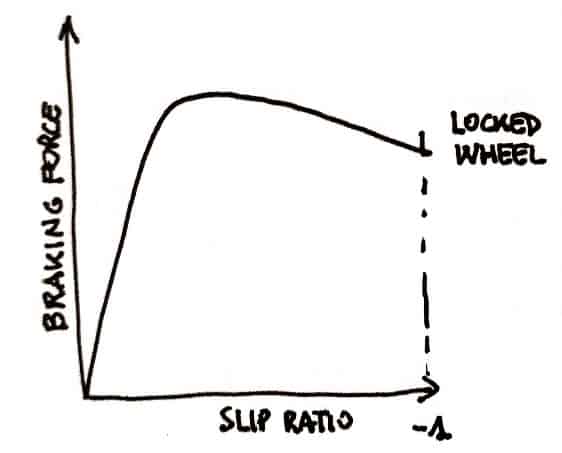
Come abbiamo detto all'inizio di questi articoli sui pneumatici, nessuna accelerazione può avvenire senza una forza che agisca tra il battistrada e il suolo in conformità con il La seconda legge di Newton e lo stesso (con direzione inversa) vale per la frenata.
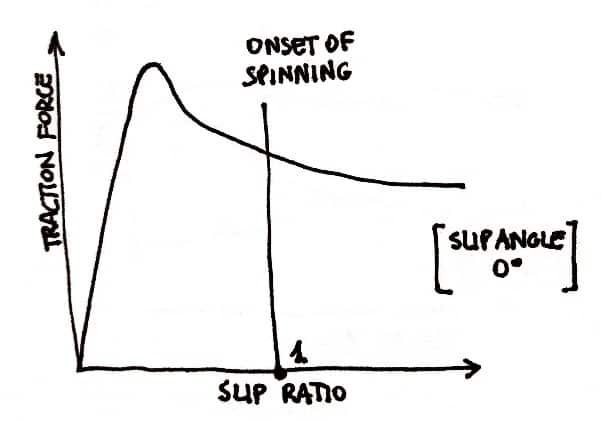
Con le forze longitudinali create dalle coppie di trazione e di frenata è fondamentale introdurre la rapporto di scorrimento.
Definizione del rapporto di slittamento.
La rapporto di scorrimento (SR) è definito come:
\(\begin{align} SR= \frac{s}{\omega_0}=\frac{\omega-\omega_0}{\omega_0}=\frac{\omega}{\omega_0}-1\end{align} \)Dove \( s=\omega-\omega_0 \) è il valore longitudinale velocità di scorrimento, ovvero la differenza tra la velocità angolare della ruota e la velocità angolare della ruota libera.
In free-rolling SR = 0, \(\frac{\omega}{\omega_0}=1\) (la velocità della ruota è uguale alla velocità della ruota libera di rotolare).
In filatura SR = 1, \(\frac{\omega}{\omega_0}=2\) (la velocità della ruota è il doppio della velocità della ruota libera di rotolare - definita in modo arbitrario).
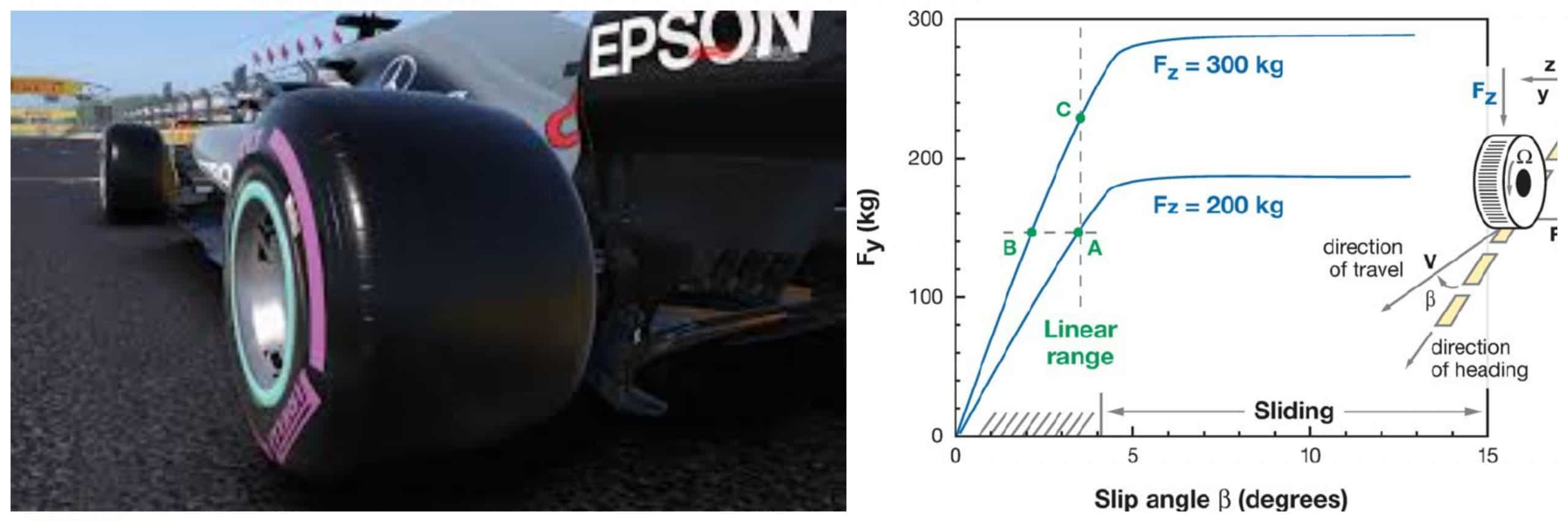
Si noti che abbiamo considerato il angolo di scorrimento α=0. Se questo non è vero, dobbiamo introdurre il termine con le velocità, importante se le forze di trazione e di frenata vengono esercitate in condizioni di curva.
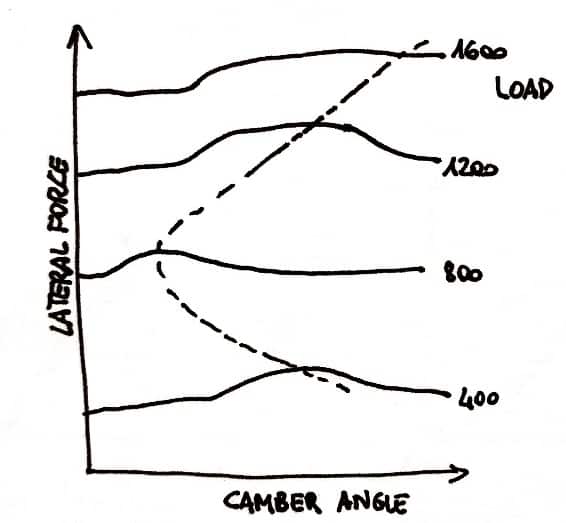
La forze di trazione o di frenata dipende dal rapporto di slittamento, come mostrato nelle immagini seguenti.
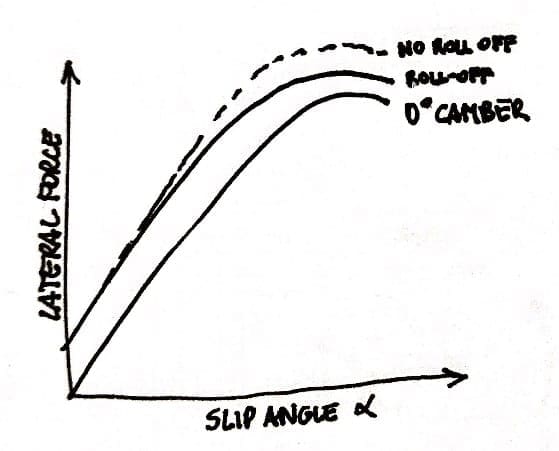
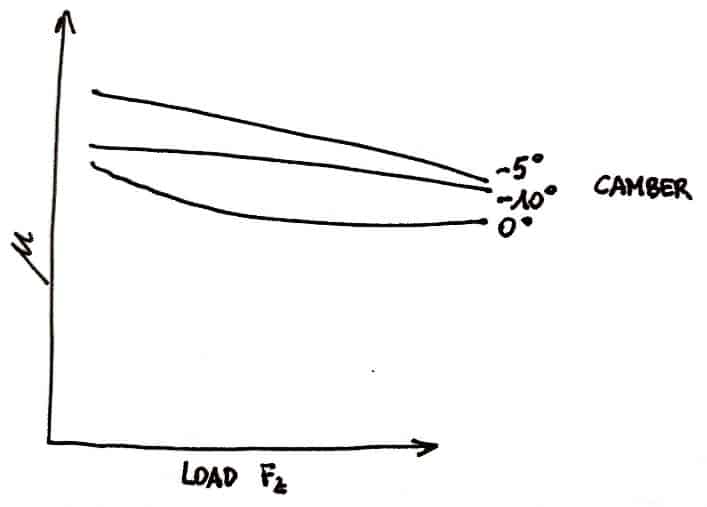
L'angolo di campanatura influisce sull'angolo di slittamento e sul rapporto di slittamento.
Come abbiamo visto nel capitolo riferito alla campanatura, una Il pneumatico bombato produce una forza laterale nella direzione dell'inclinazione. (spinta della campanatura).
Ovviamente, la campanatura provoca una distorsione laterale nell'impronta del pneumatico e questo influisce sulla scia pneumatica e quindi sulla coppia di allineamento.
A causa della diminuzione della distanza tra la prua e la poppa della stampa, il la coppia di allineamento in una ruota bombata è leggermente inferiore rispetto ad una ruota non camerata e quindi si ha una piccola destabilizzazione della coppia di allineamento che aumenta l'angolo di slittamento; ciò può richiedere un aumento della scia meccanica per produrre l'effetto di centratura del desiderio.
Utilizzando i dati raccolti, possiamo approssimare la campanatura desiderabile per la ruota anteriore esterna per una serie di carichi verticali per massimizzare Fy/Fz.
L'effetto della pressione sul rapporto di scorrimento e sull'angolo di scorrimento.
La pressione degli pneumatici è una delle più semplice e più comunemente modificato nella messa a punto di un'auto da corsa. La gamma di pressioni ammissibili è spesso stabilita dal produttore del pneumatico.
Con la pressione possiamo gestire la rigidità degli pneumatici; se la pressione degli pneumatici viene aumentata la carcassa si più rigida e quindi la rigidità in curva aumenterà.
Riducendo la pressione di contatto tra il battistrada in gomma e la strada si aumenta il coefficiente di attrito effettivo, e aumenta le dimensioni dell'impronta e riduce la pressione di contatto nella stampa..
Tuttavia, una pressione dell'aria troppo bassa crea aree di alta pressione localizzate ai lati della stampa a causa della rigidità del fianco. L'idea generale è quella di impostare la pressione dell'aria in modo che il battistrada centrale e i bordi del battistrada sopportino una quota proporzionale del carico.
Quando la pressione diminuisce, l'impronta si allunga e il centro della forza laterale si sposta all'indietro. Quando uno pneumatico perde aria, sforzo di guida per una data accelerazione laterale in curva aumenta a causa della diminuzione della rigidità in curva e della aumento della coppia di allineamento.
La resistenza aerodinamica dei pneumatici sarà diminuisce con l'aumento della pressione.
Qual è la migliore pressione degli pneumatici per l'angolo di slittamento e il rapporto di slittamento?
La pressione migliore per gli pneumatici è un compromesso tra molti fattori, il Le migliori prestazioni si ottengono con pressioni più elevate, la migliore aderenza con pressioni inferiori e la pressione ottimale può essere trovata solo con la sperimentazione.
La pressione differisce dalla campanatura (ad esempio) perché non è un valore costante durante la gara o in generale durante il rotolamento dello pneumatico. Questo è il motivo per cui di solito si parla di pressione a caldo e pressione a freddo, riferito alla pressione a regime e alla pressione gonfiata nel pneumatico prima della sessione.
Quindi, meccanici e ingegneri definiscono la pressione ottimale a freddo, ovvero la pressione che in condizioni di pieno funzionamento raggiungere la pressione ottimale a caldo indicata dal produttore del pneumatico.
Esempio di auto a trazione FW.
Parlando di auto da turismo a trazione anteriore, ecco un esempio di pressione degli pneumatici (noi parliamo di valori in "bar", ma in F1 e in altri campionati i valori sono indicati in "psi"):
| Pressione a freddo (bar) | Pressione a caldo (bar) | |
| F slick | 1.40 | 2.10 |
| R slick | 1.70 | 2.10 |
| F pioggia | 1.80 | 2.20 |
| Pioggia di R | 2.00 | 2.20 |
Le pressioni possono essere differenza tra pneumatici anteriori e posterioriLe prime sono responsabili della trazione e dello sterzo, quindi si riscaldano più velocemente (e di più) delle seconde.
Di solito i pneumatici da pioggia hanno una struttura diversa e quindi la loro pressione ottimale può essere diversa da quella dei pneumatici slick. Si noti che le condizioni della pista, l'aderenza, le temperature dell'aria e la marca degli pneumatici possono modificare notevolmente i valori riportati nella tabella.
L'effetto della temperatura sull'angolo di scorrimento e sul rapporto di scorrimento.
La temperatura dei pneumatici influisce sia la capacità di produrre forza del pneumatico e anche la sua durata. Una variazione di temperatura modifica il modulo di elasticità della gomma e c'è una variazione di temperatura. valore ottimale per la massima aderenza. La temperatura varia in base alle condizioni della pista e alla pressione del pneumatico.
Solo per dare qualche numero, in auto da corsa da turismo un classico esempio di buon pneumatico riscaldato (anche con un angolo di campanatura adeguato) è dato da 105°C gradi nella zona interna del battistrada, 95°C in quella centrale e 85°C in quella esterna.