Modellazione del comportamento del pneumatico - Modelli pratici
La Formula Magica e i modelli di pneumatici a spazzola
Come modellare il comportamento del pneumatico: modello a spazzola del pneumatico.
Come abbiamo visto nei capitoli precedenti, è molto difficile descrivere con precisione il comportamento dei pneumatici ed è per questo che gli ingegneri utilizzano alcuni modelli che cercano di gestire l'effetto delle forze su di essi".ruote in gomma".
Si discute dell'analisi delle proprietà di un modello teorico di pneumatico relativamente semplice attraverso una rappresentazione meccanica.
Questo è il caso del Modello di pneumatico a spazzole, molto utile per capire il comportamento del pneumatico grazie alla sua distribuzione parabolica della pressione..
Quattro fattori fondamentali giocano un ruolo in questo modello: proprietà di attrito nell'interfaccia strada-pneumatico, distribuzione della pressione normale di contatto, cedevolezza della gomma del battistrada e cedevolezza della cintura/carcassa.
I fondamenti del modello di pneumatico a spazzola.
Il modello più semplice è dato da considerando una carcassa rigidama ne esistono anche di più complessi, in cui il nastro viene paragonato a una trave o a una corda. Se la rappresentazione del nastro è data da una corda tesa invece che da una trave elastica, il modello di equazione differenziale appartiene al secondo ordine e non al quarto.
Parametri del pneumatico modello spazzola.
Quando il i parametri del modello sono scelti in modo appropriato, la scelta del tipo di modello di carcassa ha solo un effetto limitato. Il modello a carcassa rigida con elementi elastici del battistrada ha una semplicità e una corrispondenza qualitativa con il comportamento sperimentale del pneumatico. Considereremo solo una deflessione uniforme della carcassa per migliorare la rappresentazione della coppia di allineamento in caso di slittamento combinato.
Il modello di pneumatico a spazzole è costituito da una fila di setole elastiche che tocca il piano stradale e può essere deflessa in una direzione parallela alla superficie stradale. La loro conformità rappresenta l'elasticità della combinazione di carcassa, cintura ed elementi del battistrada del pneumatico reale.
Modello di pneumatico formula a spazzole.
Durante il rotolamento del pneumatico, il primo elemento che entra nel si ipotizza che la zona di contatto sia perpendicolare rispetto alla superficie stradale. Quando il pneumatico rotola liberamente (senza forze di trazione o di frenata) e senza slittamento laterale, campanatura o rotazione, la ruota si muove lungo una linea retta parallela alla strada e in direzione del piano della ruota. In questa situazione, gli elementi del battistrada rimangono verticali e si muovono dal bordo d'attacco a quello d'uscita senza sviluppare una deviazione orizzontale e, di conseguenza, senza generare una forza di prua e di poppa o una forza laterale..
Per ulteriori letture e dettagli si veda questo articolo pdf.
Quando il il vettore velocità ruota V mostra un angolo rispetto al piano della ruotasi verifica uno slittamento laterale.
\(\begin{align*} \Omega\cdot r_e=V\cdot \cos\alfa \neq V \end{align*} \)Modello a spazzola e pneumatico Magic formula.
La massima deflessione possibile che può essere raggiunta dalla a seconda della sua posizione nella regione di contatto. Questo massimo è governato dalla costante coefficiente di attrito \( \mu \) , la verticale distribuzione della forza \( q_z \) e il rigidità dell'elemento \( c_{py} \) . Si è ipotizzato che la distribuzione della pressione e di conseguenza anche la deflessione massima varino secondo una parabola.
Non appena la linea retta di contatto interseca la parabola, inizia lo scivolamento.
Introduciamo il punto di slittamento S, che è un punto immaginario collegato alla ruota e si trova, nell'istante considerato, a una distanza pari al raggio di rotolamento effettivo \( r_e \) sotto il centro della ruota.
A rotolamento libero, per definizione, il il punto di slittamento S ha una velocità pari a zero.
Dove \( V_r \) è la velocità di rotolamento.
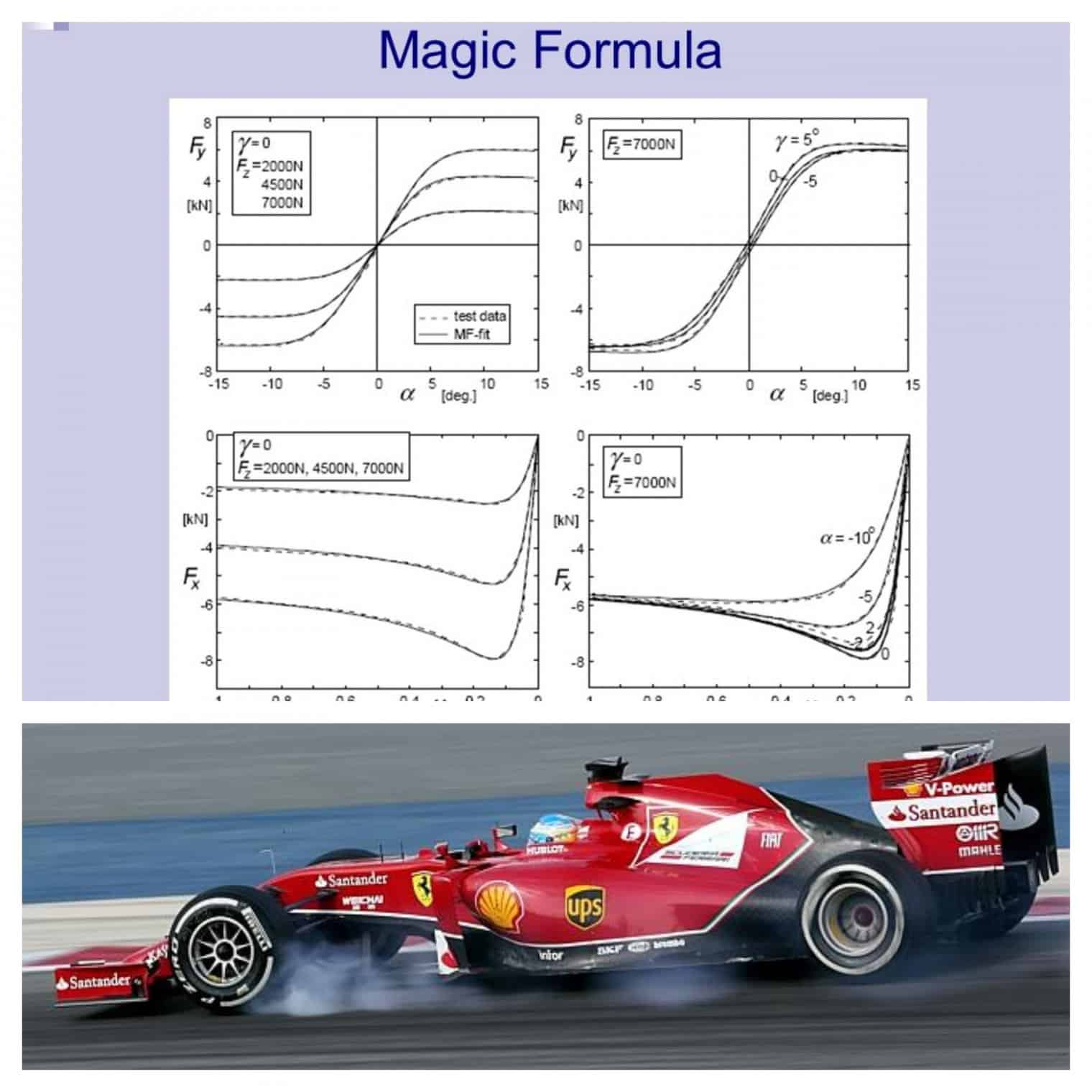
Modellazione dei pneumatici: il modello di pneumatici MAGIC Formula.
Il pneumatico Magic Formula è un modello semi-empirico di pneumatico ampiamente utilizzato per calcolare caratteristiche di forza e momento del pneumatico allo stato stazionario per l'uso nella dinamica del veicolo studi. Per le nozioni di base sull'applicazione dell'interazione pneumatico-strada in Matlab controlla qui.
La forma generale della formula per determinati valori di carico verticale e angolo di campanatura è:
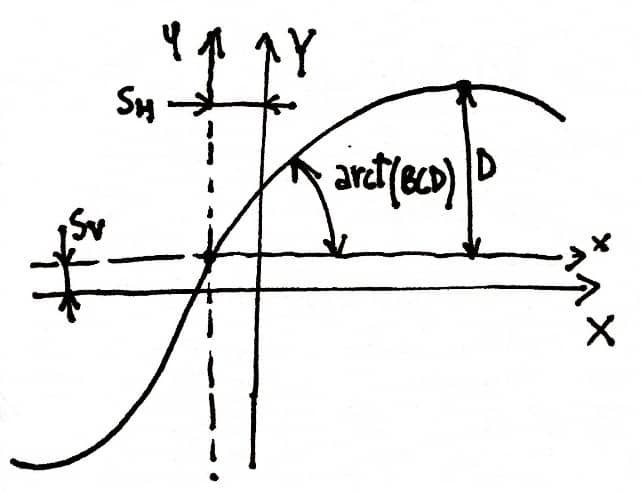
\( \begin{align*} y=D\cdot \sin[C\cdot\arctan(B\cdot x-E\left{B\cdot x- \arctan{B\cdot x}\right{]\end{align*} \)Dove:
\( Y(X)= y(x)+S_v \) variabile di uscita \( F_x, F_y, F_z \)
\( x= X+S_h \) variabile di input \( \alfa \) o \( \tanalfa \)
\( B \) = fattore di rigidità
\( C \) = fattore di forma
\( D \) = valore di picco
\( E \)= fattore di curvatura
\( S_H \) = spostamento orizzontale
\( S_V \) = spostamento verticale
La Formula magica \( y(x) \) produce tipicamente una curva che passa per l'origine \( x=0, y=0 \) , raggiunge un massimo e successivamente tende ad un asintoto orizzontale.