Air Flow Measurement: hot wire anemometer
Experimental aerodynamics: how hot wire anemometer tecnique works
Air flow measurement and hot wire anemometer.
In the study of experimental aerodynamics, it is necessary to know the speed of the flow and to have indications on the air flow (in our case) that surrounds a body.
The flow meter is the instrument for measuring the flow rate, volumic or mass, of a fluid, liquid or aeriform.
What is a hot wire anemometer?
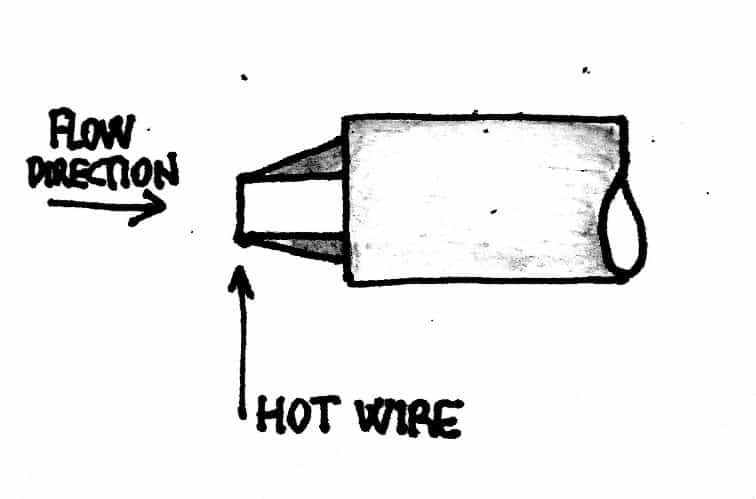
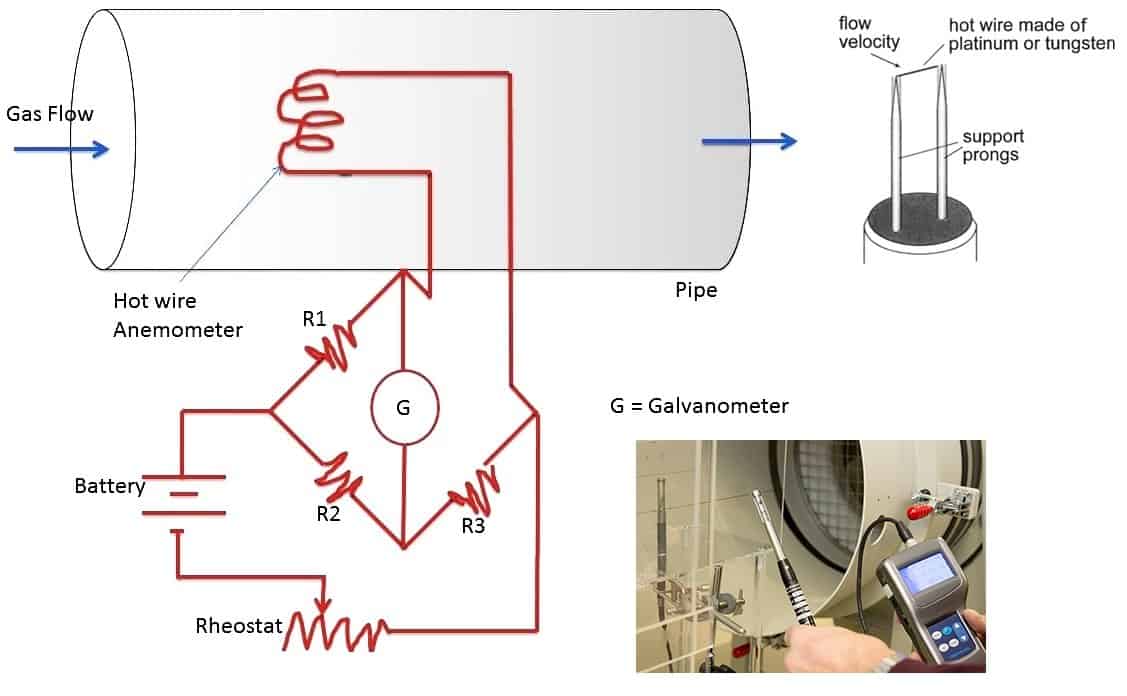
The hot wire anemometer is precisely a static flow meter, normally used to determine the air speed in ventilation ducts. It is composed of a resistance thermometer, that means a resistance whose value is proportional to the temperature, which is fed by an electric current of known intensity, such as to bring it to a temperature higher than that of the fluid to be measured. This resistance is immersed in the fluid whose speed is to be measured. The fluid will cool the resistance proportionally to its speed allowing it to go back to it.
The advantages of this instrument are mainly due to the very small dimensions that can be taken by the probe. This allows you to make measurements in various positions in the pipe, to disturb the flow of the fluid in a minimal way, to have a very high response speed (in the order of kHz) that allows you to detect the speed variations due to turbulence.
The disadvantages are related to the dependence of the calibration on various factors such as the characteristics of the fluid, its pressure and its temperature.
How the hot wire anemometer works?
The operating principle of HWA – Hot Wire Anemometer – at constant wire temperature is positioned with an axis perpendicular to the current speed of a known flow. The probe allows to measure instantaneous physical quantities (which vary over time). A hot wire probe is indispensable for detecting, for example, the fluctuations present in the turbulent boundary layer or also instantaneous quantities in other turbulent flows such as the jet and the wake.
To perform this function, hot wire anemometry must meet the following requirements:
- Low intrusiveness: the dimensions of the probe must be as small as possible in order to be able to make instantaneous measurements in motion fields, even of small dimensions, so as not to induce alterations on the field itself;
- High spatial resolution: the goal is not to measure integral physical quantities, therefore averaged, therefore the measurement must be as precise as possible;
- High frequency response: the instrument must respond quickly to the fastest fluctuations over time of the fluid dynamic quantities to be measured;
- High sensitivity: the electrical signal output from the anemometer, for the same fluid dynamic quantity to be analyzed, must be as high as possible, in order to obtain a very accurate and therefore very precise measurement in order to detect changes over time;
- High Sound / Noise ratio: each fluctuation is characterized by a certain value of this ratio, therefore for this technique it must be sufficiently high so as not to have alterations in the detection;
- Voltage signal output from the anemometer continuously over time.
Which are the problems related to the air flow measurement with the hot wire anemometer?
- Need for calibration of the instrument: the output signal is electric, therefore, whatever the fluid dynamic quantity to be detected, it is essential to find the coefficients representative of the link between the electrical signal and the quantity under test;
- Ambiguity of the sensor: the hot wire probe is not able to identify the direction of speed (only the module can be detected), therefore it is necessary to locate several hot wire probes in appropriate positions to obtain a complete measurement;
- Voltage response of the non-linear hot wire anemometry system: this non-linearity obviously makes it impossible to match the average voltage value at the output of the anemometer with the average value of the physical quantity measured unlike the pressure transducers considered in the previous exercises;
- Temperature effect: since the hot wire probe is characterized by an electrical resistance, if the calibration is performed in certain ambient conditions, while the measurement is carried out in other ambient conditions, it will be necessary to make corrections on the parameters obtained from the calibration, being the resistance electric dependent on temperature.
We summarized the operating principle of this technique: hot wire anemometry is based on the Joule effect induced on the sensor, therefore kept hot, and on forced convection (neglecting the effects of the other heat exchange mechanisms), for which it is responsible the current of fluid, which hits the wire with a certain electrical resistance.
The working principle of a hot wire anemometer.
In other words, the operation of a hot wire probe is based on the variation in the electrical resistance of a tungsten filament consequent to the temperature variation induced by the forced convection cooling of the wire heated by Joule effect by means of a suitably designed electric circuit.
Therefore, the following expressions representative of the phenomenon just described can be considered schematically:
- Heating by Joule effect: the electrical resistance of the sensor depends on the temperature:
RW = R0 [1 + b (TW −T0)]
– RW: electrical resistance of the sensor at TW temperature,
– R0: electrical resistance of the sensor at the temperature T0 supplied by the manufacturer,
– TW: temperature of the heated wire,
– T0: reference temperature supplied by the manufacturer.
The costant current imposed on a hot wire anemometer.
By imposing the passage of an electric current I through a circuit equipped with a servo amplifier, the power dissipated in thermal power by Joule effect is expressed as follows:
PJoule = RwI2
- Forced convection cooling: the fluid current removes heat from the wire:
Pconv = h (πdl) (Tw – Tf)
Where:
– h: heat transfer coefficient for forced convection, it depends on the speed of the current,
– Tf: fluid temperature.
Since the heat exchange coefficient h depends on it, the speed of the current contributes to defining the extent of the cooling. Before heating the probe, it is at the same temperature of the fluid, therefore it is characterized by an electrical resistance Rf, which can be calculated, similarly to what was done previously, in the following way:
Rf = R0 [1 + b (Tf – T0)]
- Cooling by natural convection: the removal of heat by this heat exchange mechanism becomes comparable to that of forced convection only in the case of low fluid speeds and depends on the temperature difference between TW and Tf (this contribution is generally neglected)
- Cooling by radiation: the removal of heat by this heat exchange mechanism becomes relevant in the case in which TW> 300°C, therefore this contribution is generally neglected because it remains around temperatures TW ≈ 250°C.
In stationary condition (neglecting the presence of transients) the heat produced by Joule effect is equal to that removed by forced convection (neglecting the other heat exchange mechanisms), therefore the following equilibrium thermal equation applies:
RWI2 = h (πdl) (TW −Tf)
King’s Law: costant current hot wire anemometer.
Dimensional analysis to obtain the King’s law.
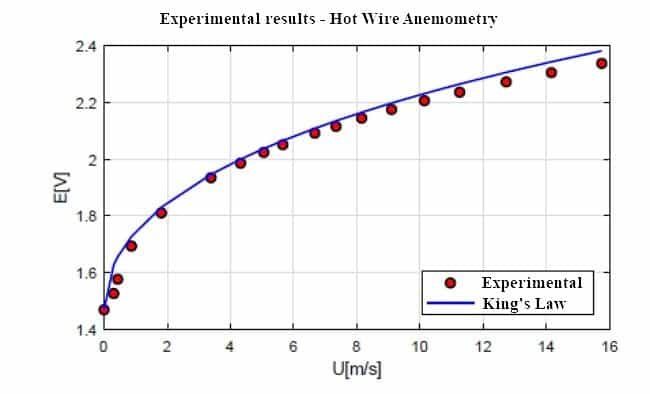
Starting from this equation, introducing the dimensionless parameters that govern the phenomenon in question (such as the Nusselt Nu number, the Prandtl Pr number, the Reynolds Re number and so on) after performing the dimensional analysis of the problem by applying the Buckingham’s theorem, and exploiting Ohm’s law and some empirical relationships, such as Kramers’ law, we reach the so-called King’s law, which connects the voltages E measured at the ends of the electrical resistance to the velocities V of the current, in the following way ( note the nonlinear link between E and V):
E2 = A + BVn
Where A, B and n are constants that are obtained during the calibration phase. Since the system at constant temperature TW, when measuring at speed V = 0 m/s, since the speeds are known during calibration, the offset signal E0 is obtained, which is representative of a power; in particular it is noted that:
E02 = A
The power of which parameter A is representative cannot derive from forced convection, since the speed of the current is zero, therefore it is the power linked to the energy removed by natural convection, having a system that continues to work at the TW temperature even though there is no is a cooling induced by the forced convection produced by the fluid stream. In general, it is good to remember that the amount of heat exchange between the filament and the current, therefore the voltage measured across the sensor, does not depend only on the module of the speed V of the current, but also on the incidence α and β with which it is invested:
E = f1(V) f2(α) f3(β)