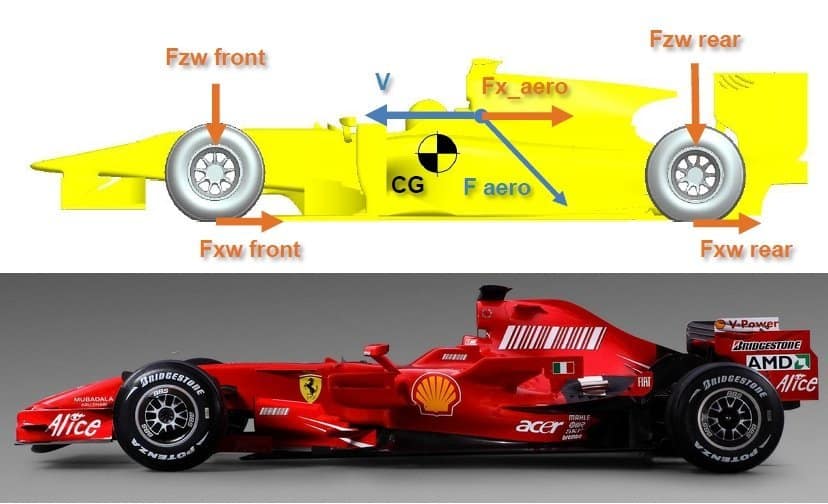
How lift and drag force are generated in Racing cars
Drag force and lift force definition and mathematical explanation
Drag force and Lift force.
In this lesson (for the previous one about aerodynamic coefficients check here) the concept of aerodynamic lift and drag force will be introduced. Since these are basic notions, the reader who is already practical with these concepts may skip this lesson. Let’s talk about two of the most important outcomes of a fluid-dynamics analysis!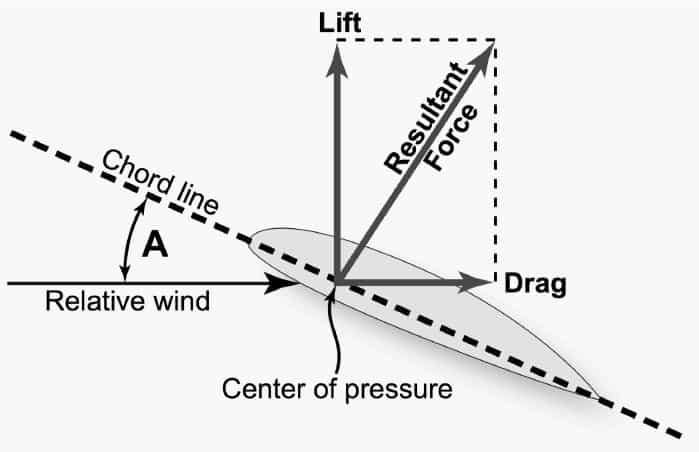
How is drag and lift force generated: the pressure explanation.
In general, the interaction of the fluid (i.e. air) with the body (i.e. airfoil) produces a resultant force on it. For the action-reaction principle, the same force with opposite sign is experienced by the fluid in motion. The component of that resultant aligned with the flow is called DRAG FORCE, while the one perpendicular to flow direction is referred as LIFT FORCE. Physically the total resultant which can be projected according to the preferred reference system, is built up by the sum of the pressure forces and shear stresses acting on the body surface. As we see from the image, the integral of these actions gives us the forces (and the moment) acting on the specific body.
How is drag and lift force generated: the second law of dynamics.
We’re not here to spend to much time on formulas but we can notice that on the left side we have the inertia forces while on the left side we have pressures forces and viscous forces. The second equation reported is the transcription of the second law of dynamics for fluids. The equation has been simplified (also a term with the divergence of the velocity should appear) assuming incompressible fluid. In fact, the first equation states the incompressibility condition of the fluid, obtained writing the mass balance equation. The density is denoted with rho, v identifies the velocity, p the pressure while mu is the dynamic viscosity of the fluid.
How is drag and lift force generated: momentum balance.
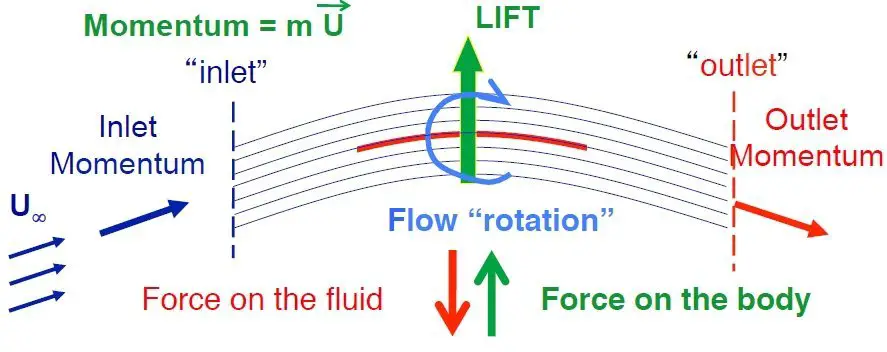
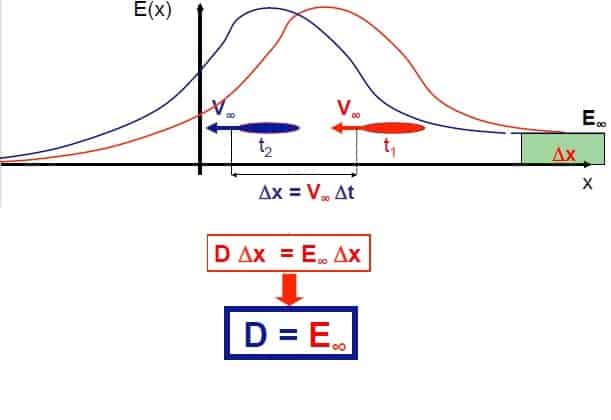
A simple view of the force exchaged between the body and the fluid is made clear in the picture below. The momentum of the fluid (a vector quantity) has changed if we compare the inlet and the otulet momentum. The momentum variation equals the force acting on the fluid. For our readers, we give also an energetic explanation of drag. Our object, moving within the fluid perturbs the field. We investigate the energy in the plane on the motion -x: its value is not zero since the vorticity of the fluid introduces a certain amount of energy in the fluid field. The energy introduced in the system equals the work done by external forces, in this case the object is moving mainly in x direction so the great part of the work is determined by the drag multiplied the distance travelled x. So we have the important hint that the drag force is closely related to vorticity introduced in the field. The more concentrated is the vorticity, the more increase in resistance we have.
The components of drag force.
The two main terms drag is made of are: viscous drag (Df) and pressure drag (Dp). The viscous term is dominant for aerodynamical shapes while the pressure terms has great impact on the total drag in bluff bodies. It’s important to point out that a streamlined body can behave as a bluff body at high angle of attack (when the boundary layer detaches).
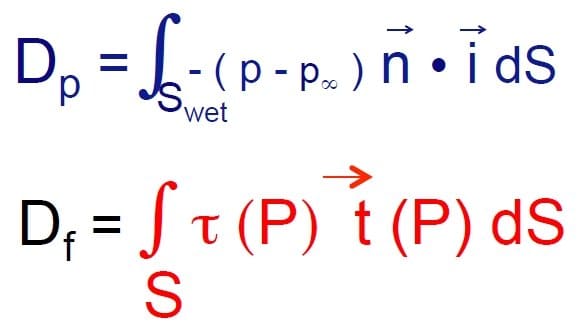The origin of lift force (downforce).
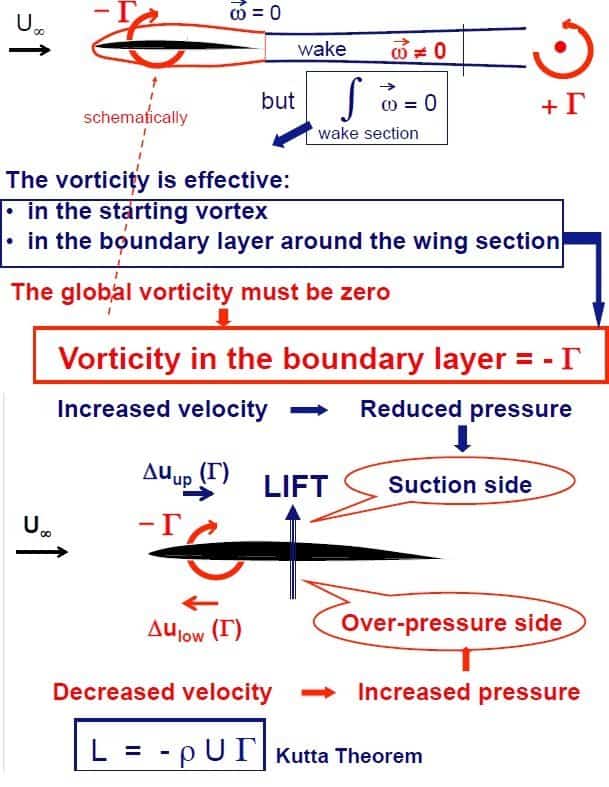
Talking about lift, we have to talk about its origin. In particular, here below, the vorticity interpretation is reported. Vorticity is essential to lift. As we get from the Kutta-Joukowsky theorem, no vorticity means no lift. Vorticity is produced by the shear friction at the wall. When a body is put inside a flow, vorticity is impulsively produced at the wall and released at the trailing edge. Wait! You’re saying the vorticity field is irrotational (they told you at the school), right!?! It is zero but on the whole domain. In fact, near the body (airfoil) and opposite vortex is produced and it is the cause of lift. The term tau in the Kutta well-known expression (2D bodies) identifices the vorticity.
Vorticity is the key for lift force generation.
So, in this lesson we’ve learned the physics beneath the drag and lift forces. Ehi, are you still asking yourself why the vorticity cannot be zero around the airfoil (within the boundary layer)? Think a bit about the definition of vorticity:
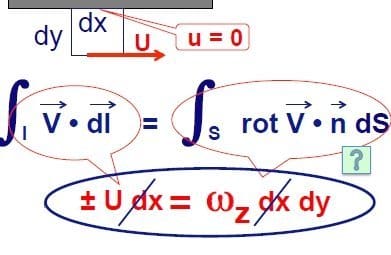Vorticity is produced at the wall due to no-slip condition. Remember that a different velocity between lower and upper sides determines a non-zero vorticity! In next lesson, we’ll introduce the notion of laminar and turbulent flows and their impact on aerodynamic coefficients.
